bookmark_border
Quasi-static crushing of the S-shaped square tube Abaqus
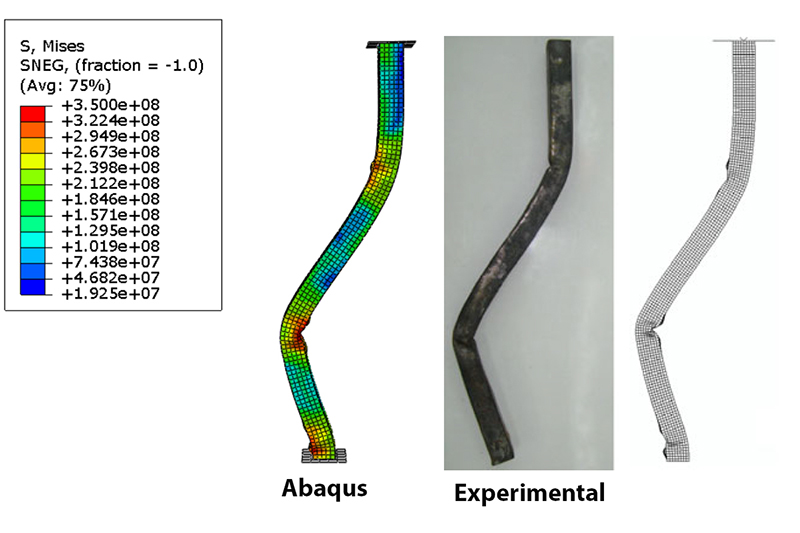
In this example we intend to simulate crushing of the S-shaped square tube in the Abaqus software
The tube is made of milled steel. the cross section of the tube is square-like and the general shape of the tube is in form of S. compressive load is applied to the top of the tube causing that to be deformed
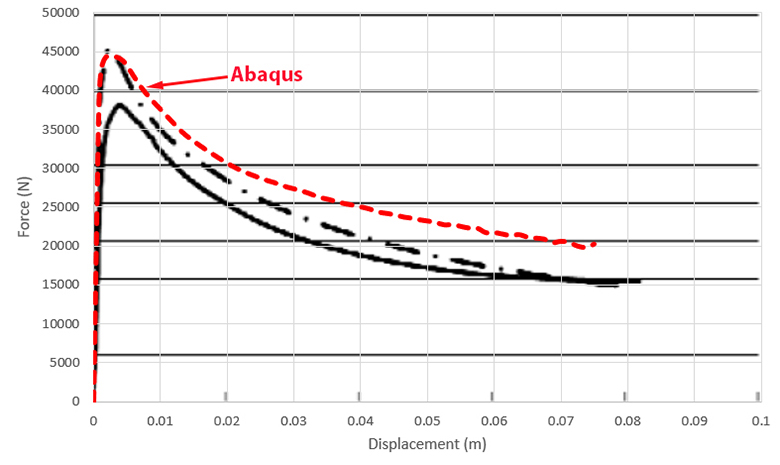
In this picture the results obtained from the Abaqus software have been compared with experimental results
In this picture the diagram of force-displacement has been drawn
This project has been validated, which means that the results obtained from Abaqus software are similar to the results of the article. In other words, this project is based on the article
Tomas(verified owner)
Very good modeling
Sikara
Very interesting results, exactly like the test sample